Формы фигуры и – как определить свой вид, каковы размерные признаки типовой женской формы, как подобрать диету и одежду
Геометрические фигуры и их названия
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках. Но обучение будет проходить наиболее эффективно в том случае, если к распечатанному заданию вы добавите еще и различные образцы геометрических фигур. Для этой цели могут подойти такие предметы, как мячики, пирамидки, кубики, надутые воздушные шары (круглые и овальные), кружки для чая (стандартные, в форме цилиндра), апельсины, книги, клубки ниток, квадратные печенья и многое другое — все, что подскажет вам фантазия.
Все перечисленные предметы помогут ребенку понять, что значит объемная геометрическая фигура. Плоские фигуры можно подготовить, вырезав из бумаги нужные геометрические формы, предварительно раскрасив их в разные цвета.
Чем больше различных материалов вы подготовите для занятия, тем интереснее будет ребенку изучать новые для него понятия.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Геометрические фигуры 1 класс — Онлайн-тренажер
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
Геометрические фигуры и их названия — Проводим занятие с ребенком:
Чтобы легко и непринужденно ребенок смог запомнить геометрические фигуры и их названия, скачайте сначала картинку с заданием во вложениях внизу страницы, распечатайте на цветном принтере и положите на стол вместе с цветными карандашами. Также к этому времени у вас уже должны быть заготовлены различные предметы, которые мы перечисляли ранее.
- 1 этап. Сначала пусть ребенок выполнит задания на распечатанном листе — проговорит вслух названия фигур и раскрасит все картинки.
- 2 этап. Необходимо наглядно показать ребенку отличия объемных фигур от плоских. Для этого разложите все предметы-образцы (как объемные, так и вырезанные из бумаги) и отойдите с ребенком от стола на такое расстояние, с которого хорошо видны все объемные фигуры, но потерялись из виду все плоские образцы. Обратите внимание малыша на этот факт. Пусть он поэкспериментирует, подходя к столу то ближе, то дальше, рассказывая вам о своих наблюдениях.
- 3 этап. Дальше занятие нужно превратить в своеобразную игру. Попросите ребенка, чтобы он внимательно посмотрел вокруг себя и нашел предметы, которые имеют форму каких-либо геометрических фигур. Например, телевизор — прямоугольник, часы — круг и т.д. На каждой найденной фигуре — громко хлопайте в ладоши, чтобы добавить энтузиазма в игру.
- 4 этап. Проведите исследовательскую и наблюдательную работу с теми материалами-образцами, которые вы заготовили к занятию. Например, положите на стол книгу и плоский прямоугольник из бумаги. Предложите ребенку пощупать их, посмотреть на них с разных сторон и рассказать вам свои наблюдения. Таким же образом можно исследовать апельсин и бумажный круг, детскую пирамидку и бумажный треугольник, кубик и бумажный квадрат, воздушный шар овальной формы и овал, вырезанный из бумаги. Список предметов вы можете дополнить сами.
- 5 этап. Положите в непрозрачный пакет различные объемные образцы и попросите ребенка достать на ощупь квадратный предмет, затем круглый, затем прямоугольный и так далее.
- 6 этап. Разложите перед ребенком на столе несколько различных предметов из тех, которые участвуют в занятии. Затем пусть ребенок отвернется на несколько секунд, а вы спрячьте один из предметов. Повернувшись к столу ребенок должен назвать спрятанный предмет и его геометрическую форму.
Скачать геометрические фигуры и их названия — Бланк задания — вы можете во вложениях внизу страницы.
Названия геометрических фигур — Карточки для распечатки
Изучая с малышом геометрические фигуры, вы можете использовать во время занятий карточки для распечатки от Лисёнка Бибуши
Первые шесть карточек дадут вам возможность изучить с ребенком такие фигуры: овал, круг, квадрат, ромб, прямоугольник и треугольник, под каждой фигурой в карточках можно прочесть ее название.
После того, как ребенок запомнил название определенной фигуры, попросите его выполнить следующее: обвести по контуру все имеющиеся на карточке образцы изучаемой фигуры, а затем раскрасить их в цвет основной фигуры, расположенной в верхнем левом углу.
Скачать названия геометрических фигур — Карточки для распечатки — вы можете во вложениях внизу страницы
Карточки для распечатки с изображением плоских геометрических фигур
С помощью следующих шести карточек ребенок сможет познакомиться с такими геометрическими фигурами: параллелограмм, трапеция, пятиугольник, шестиугольник, звезда и сердце. Как и в предыдущем материале под каждой фигурой можно найти ее название.
Чтобы разнообразить занятия с малышом, совмещайте обучение с рисованием – такой метод не даст ребенку переутомиться, и малыш с удовольствием будет продолжать учебу. Следите за тем, чтобы обводя фигуры по черточкам, ребенок не спешил и выполнял задание аккуратно, ведь подобные упражнения не только развивают мелкую моторику, они могут повлиять в дальнейшем на почерк малыша.
Скачать карточки для распечатки с изображением плоских геометрических фигур вы можете во вложениях
Объемные геометрические фигуры и их названия — скачать карточки
В процессе, того, как вы будете изучать с ребенком объемные геометрические фигуры и их названия, используя новые шесть карточек от Бибуши с изображениями куба, цилиндра, конуса, пирамиды, шара и полусферы, приобретите изучаемые фигуры в магазине, либо воспользуйтесь предметами, находящимися в доме, имеющими подобную форму.
Покажите малышу на примерах, как в жизни выглядят объемные фигуры, ребенок должен потрогать и поиграть с ними. Прежде всего, это необходимо для того, чтобы задействовать наглядно – действенное мышление малыша, с помощью которого ребенку проще познавать окружающий мир.
Скачать — Объемные геометрические фигуры и их названия — вы можете во вложениях внизу страницы
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Счет до 5 — Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ И ФОРМЫ | Введенская сторона
В этом и в следующем номере мы расскажем вам о программах и заданиях, в которых ребята знакомятся с двумя основными принципами формообразования:
геометрическим и бионическим.
Сегодняшняя статья посвящена заданиям курсов «Геометрические формы» и «Знаки творчества», где композиции создаются на основе геометрических фигур и производных от них элементов.
В последовательно выстроенной системе упражнений и заданий программы «Геометрические формы» (2-й год обучения в Дизайн-центре) за основу берутся простейшие геометрические фигуры (круг, треугольник, квадрат): дети учатся видеть эти формы в окружающей среде, использовать их в своих композициях и создавать более сложные построения на их основе.
Начинаем с исследования линий, проведенных на листе бумаги: ломаных, кривых, округлых 
– пересекающихся друг с другом и образующих замкнутые контуры геометрических фигур. Далее изучаем сами простейшие фигуры, исследуем их декоративные, конструктивные и комбинаторные свойства и особенности. Интересно наблюдать с каким энтузиазмом
наши ученики экспериментируют и изобретают всевозможные варианты деления
и построения квадратов, треугольников и кругов. Такие задания – как игра с калейдоскопом, где мы находим бесконечное количество новых комбинаций и оригинальных выразительных возможностей.
Этому интересу и неиссякаемой фантазии способствуют и разнообразные материалы, с которыми мы работаем: маркеры и фломастеры, гелевые ручки и цветные карандаши, бумага различных форматов и цветов, самоклеющаяся плёнка и обои, деревянные палочки и пластиковые трубочки, шерстяные нитки и всевозможные верёвочки, пуговицы и другие мелкие предметы.
В последующих заданиях дети учатся выделять простейшие геометрические формы, лежащие в основе более сложных, в том числе природных форм, или наоборот, получать сложные объекты, составляя их из простых геометрических элементов, например, фигур одного типа. Применяя технику мозаики, геометрические сетки, текстуры и паттерны, создаём мозаичные изображения животных, стилизованные портреты, натюрморты и архитектурные фантазии.
Пропедевтические упражнения, чередующиеся с творческими заданиями, закладывают основы композиционного мышления, развивают внимание и исследовательские способности детей, пространственное воображение, чувство цвета и гармонии, прививают культуру работы с различными средствами выразительности, учат добиваться высокого качества работ.
Познакомившись с основами геометрического формообразования, мы используем его впоследствии как инструмент во многих заданиях и программах на более
старших курсах, в частности, в программе «Знаки творчества».
Образовательные программы:
«Геометрические формы», 2-й год обучения в Детском дизайн-центре,
«Знаки творчества», 4-й год обучения в Детском дизайн-центре.
Автор программ: Галина Корнева.
Педагоги: Галина Корнева, Елена Ковалёва, Александра Савельева, Екатерина
Лысенкова, Наталья Шенберг, Елизавета Гришина, Надежда Зарецкая.
Коллективный проект: «Новогодняя ёлка»
Задание: «Структура геометрической фигуры»
Авторы работ: Немова Алиса, Максимова Карина,
Новожилова Настя, Соколова Полина.
Возраст: 9-12 лет.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер. Такое развивающее занятие способствует более эффективному запоминанию геометрических фигур, так как здесь ребенок не только визуально их запоминает, но и с помощью логического мышления меняет их главные свойства, «обрабатывая» фигуры на волшебной фабрике.
Свойства геометрических фигур для дошкольников — Волшебная фабрика
Для того, чтобы менять свойства геометрических фигур на нашей волшебной фабрике, сначала ознакомьтесь с инструкцией, скачайте бланки заданий, распечатайте их и подготовьте для игры простой карандаш, ластик и цветные карандаши трех цветов — зеленый, красный и синий. Затем взрослый объясняет ребенку правила игры.
«Сейчас мы с тобой начинаем работать на фабрике. Здесь находятся специальные машины, которые меняют различные характеристики фигур: цвет, форму или размер. Каждая фигура, которая попадает в эту машину, проходит обработку по строгой инструкции и выходит уже измененной.»
После этого взрослый показывает пример, как работает машина на этой фабрике, изменяющая цвет фигур:
Затем взрослый объясняет ребенку принцип работы такой машины: «Любая фигура зеленого цвета, попадающая в машину, меняет цвет на красный (от зеленого круга с буквой «З» стрелочка ведет к красному кругу), любая фигура красного цвета — меняется на синий, а синяя фигура меняется на зеленый цвет.
На фабрике есть и другие машины, которые меняют другие свойства геометрических фигур — не цвет (как в рассмотренном примере), а форму или размер. Изменения с фигурами происходят по аналогичному принципу (следим за стрелочками, которые показывают, на какие фигуры должны поменяться заданные).
Также в некоторых бланках встречаются машины, которые меняют не одно свойство фигуры, а сразу два — например, цвет и форму или форму и величину.
Скачать задания — Свойства геометрических фигур — вы можете во вложениях внизу страницы
В этих заданиях нужно поменять только одно свойство фигур — их цвет. Не забудьте раскрасить фигуры слева до того, как дать ребенку задание.
В следующем задании нужно поменять другое свойство геометрических фигур — их форму. Овал меняется на прямоугольник, прямоугольник — на ромб, ромб — на овал. Будьте внимательны! Овалы и прямоугольники в задании разные — горизонтальные и вертикальные. Менять нужно именно такие, какие нарисованы в машине. Обязательно раскрасьте фигуры слева, прежде чем начинать работу.
В данном задании заданная фигура сначала меняет свою форму (в первой машине), а затем и свой цвет (вторая машина).
В следующем задании машины изменяют величину фигур: большие квадратики на маленькие, маленькие треугольники на большие.
На следующих машинах мы меняем сначала форму фигур, а затем их величину.
В этом задании фигуры меняют на первой машине свой цвет, а на второй машине — величину.
Ну и последнее задание самое сложное. Здесь обработка свойств фигур проходит на трех машинах. Первая машина изменяет цвет входящих геометрических фигур, вторая машина изменяет размер некоторых фигур, а третья машина завершает обработку, меняя их форму.
Группы геометрических фигур по их признакам
В этом задании вы найдете группы геометрических фигур, каждая из которых объединяет в себе фигуры по какому-то определенному признаку. Например, по цвету, форме или размеру. Ребенок должен определить по какому именно признаку разбиты фигуры в каждой группе. Подобные занятия развивают логико-математические способности детей.
Скачайте и распечатайте бланки с заданиями, дайте ребенку и объясните ему правила для выполнения упражнения: «Посмотри, здесь нарисованы геометрические фигуры, которые разбиты на несколько групп. В каждой группе фигуры объединяет какое-то одно свойство или признак. Например, в группе присутствуют все фигуры одного цвета (серый, белый или черный), одной формы (треугольник, квадрат или круг) или одного размера (маленькие, средние или большие).
Если ребенку трудно выполнять данное упражнение самостоятельно, то помогите ему встречными вопросами: «Какие геометрические фигуры ты видишь на странице? Чем они отличаются между собой? Что у них общего?»
Очень важно проводить такие занятия систематически, используя подручные материалы. Например, можно использовать пуговицы различной формы (квадратные, круглые, овальные, ромбовидные и другие), разных цветов, с разным количеством дырочек. Принцип выполнения задания тот же, что и в представленных бланках. Взрослый раскладывает на столе пуговицы, разделяя их на группы по определенному признаку. А ребенок должен определить, что общего в этих группах. Занятие будет более эффективным, если ребенок будет не только находить признаки групп, но и сам, по просьбе взрослого, будет объединять предметы в разные группы по заданным признакам.
Скачать бланки заданий — Группы геометрических фигур — вы можете во вложениях внизу страницы.
Бланк №1
Бланк №2
Бланк №3
Свойства объемных геометрических фигур — Лестница превращений
Здесь вы найдете занятие, с помощью которого ребенок научится различать свойства объемных геометрических фигур: цвет, форму и размер. Занятие представлено в двух вариантах сложности: легком (для детей от 4 лет) и усложненном (для детей от 5-6 лет). Легкий вариант задания — в бланке №1, а усложненный — в бланке №2. В бланках №3 и №4 вы можете посмотреть правильные ответы. Подготовьте цветные карандаши, распечатанные бланки с заданиями и объясните ребенку правила выполнения упражнений:
«Посмотри внимательно на картинку. Здесь изображена лестница превращений геометрических фигур. Начиная с самой нижней ступеньки каждая фигура с переходом на следующую ступеньку меняет какое-либо одно свое свойство: цвет (белый, серый или черный), форму (куб, конус или шар) или величину (большую или маленькую). Например, вот этот большой белый шар (взрослый показывает пример превращений щара на бланке №1) на второй ступеньке меняет свой размер и становится маленьким, на третьей ступеньке меняет цвет с белого на черный, на четвертой — опять становится большим, на пятой ступеньке у него меняется форма и он превращается в конус.»
Пусть ребенок некоторое время проанализирует превращения белого шара на данном примере, чтобы понять логику превращений фигур в задании. В процессе выполнения задания ребенок должен комментировать и обосновывать свои решения и действия.
Если ребенку понравилось занятие, то можно предложить ему самостоятельно нарисовать еще одну фигуру на нижней ступеньке и нарисовать цветным карандашом путь ее превращений. Аналогично можно нарисовать еще одну такую лестницу, а ребенок уже сам нарисует на ней заданные фигуры и попробует заполнить фигурами все ступеньки, руководствуясь теми же самими правилами, как в распечатанном задании.
Скачать задание на свойства объемных фигур вы можете во вложениях внизу страницы
Бланк №1 — Легкий вариант
Бланк №2 — Усложненный вариант
Бланк №3 — Правильные ответы на легкий вариант
Бланк №4 — Правильные ответы на усложненный вариант
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм.
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Геометрические фигуры из бумаги — Вырезаем и занимаемся
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Устный счет в пределах 10 — Картинки с заданиями
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Список правильных многомерных многогранников и соединений — Википедия
| Правильные (2D) многоугольники | |
|---|---|
| Выпуклые | Звёздчатые |
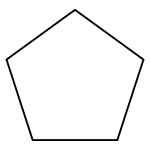 {5} |  {5/2} |
| Правильные 3D-многогранники | |
| Выпуклые | Звёздчатые |
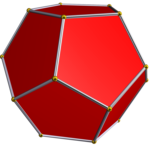 {5,3} |  {5/2,5} |
| Правильные 2D-замощения | |
| Евклидовы | Гиперболические |
 {4,4} |  {5,4}[en] |
| Правильные 4D-многогранники | |
| Выпуклые | Звёздчатые |
 {5,3,3} |  {5/2,5,3}[en] |
| Правильные 3D-замощения | |
| Евклидовы | Гиперболические |
 {4,3,4} |  {5,3,4} |
Эта страница содержит список правильных многомерных многогранников (политопов) и правильных cоединений этих многогранников в евклидовом, сферическом и гиперболическом пространствах разных размерностей.
Символ Шлефли описывает каждое правильное замощение n-сферы, евклидова и гиперболического пространства. Символ Шлефли описания n-мерного многогранника равным образом описывает мозаику (n-1)-сферы. Вдобавок, симметрия правильного многогранника или замощения выражается как группа Коксетера, которые Коксетер обозначал идентично символам Шлефли, за исключением разграничения квадратными скобками, и эта нотация называется нотацией Коксетера[en]. Другой связанный символ — диаграмма Коксетера — Дынкина, которая представляет группу симметрии (без помеченных кружком узлов) и правильные многогранники или замощения с обведённым кружком первым узлом. Например, куб имеет символ Шлефли {4,3}, с его октаэдральной симметрией[en] [4,3] или 
, представляется диаграммой Коксетера 
.
Правильные многогранники сгруппированы по размерности, а затем по форме — выпуклые, невыпуклые и бесконечные. Невыпуклые виды используют те же вершины, что и выпуклые, но имеют пересекающиеся фасеты (грани максимальной размерности = размерности пространства – 1). Бесконечные виды замощают евклидово пространство на единицу меньшей размерности.
Бесконечные формы можно расширить до замощения гиперболического пространства. Гиперболическое пространство подобно обычному пространству, но параллельные прямые с расстоянием расходятся. Это позволяет вершинным фигурам иметь отрицательные угловые дефекты. Например, в вершине может сходиться семь правильных треугольников, лежащих на плоскости. Это нельзя осуществить на обычной (евклидовой) плоскости, но можно сделать при некотором масштабе на гиперболической плоскости.
Многогранники, удовлетворяющие более общему определению и не имеющие простых символов Шлефли, включают правильные косые многогранники и бесконечноугольные правильные косые многогранники с неплоскими фасетами или вершинными фигурами.
Таблица показывает сводку правильных многогранников по размерностям.
| Конечные | Евклидовы | Гиперболические | Соединения | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Разм. | Выпук- лые | Звёзд- чатые | Косые | Выпук- лые | Компак- тные | Звёзд- чатые | Параком- пактные | Выпук- лые | Звёзд- чатые |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | ∞ | ∞ | ∞ | 1 | 1 | 0 | 0 | ∞ | ∞ |
| 3 | 5 | 4 | ? | 3 | ∞ | ∞ | ∞ | 5 | 0 |
| 4 | 6 | 10 | ? | 1 | 4 | 0 | 11 | 26 | 20 |
| 5 | 3 | 0 | ? | 3 | 5 | 4 | 2 | 0 | 0 |
| 6 | 3 | 0 | ? | 1 | 0 | 0 | 5 | 0 | 0 |
| 7 | 3 | 0 | ? | 1 | 0 | 0 | 0 | 3 | 0 |
| 8 | 3 | 0 | ? | 1 | 0 | 0 | 0 | 6 | 0 |
| 9+ | 3 | 0 | ? | 1 | 0 | 0 | 0 | * | 0 |
* 1, если размерность имеет вид 2k − 1, 2, если размерность является степенью двойки, 0 в противном случае.
Не существует правильных звёздчатых замощений в евклидовом пространстве любой размерности.
| Диаграмма Коксетера — Дынкина представляет зеркальные «плоскости» как узлы, и помещает кружок вокруг узла, если точка не лежит на плоскости. Отрезок, { }, — это точка p и зеркальный образ точки p, а также отрезок между ними. |
Одномерный многогранник (1-многогранник) — это замкнутый отрезок, ограниченный двумя конечными точками. 1-многогранник является правильным по определению и представляется символом Шлефли { }[1][2] или диаграммой Коксетера с единственным помеченным кружком узлом, . Норман Джонсон[en] дал им название дайтел и символ Шлефли { } [3].
Будучи тривиальным в качестве многогранника, дайтел возникает в качестве рёбер многоугольников и многогранников[4]. Он используется в определении однородных призм (как в символе Шлефли { }×{p}) или в диаграмме Коксетера 
как прямое произведение отрезка и правильного многоугольника [5].
Двумерное пространство (многоугольники)[править | править код]
Двумерные многогранники называются многоугольниками. Правильные многоугольники имеют равные стороны и вписаны в окружность. Правильный p-угольник представляется символом Шлефли {p}.
Обычно только выпуклые многоугольники считаются правильными, но звёздчатые многоугольники наподобие пентаграммы можно также считать правильными. Они используют те же вершины, что и выпуклые формы, но соединение происходит другим путём, при котором окружность обходится более одного раза.
Звёздчатые многоугольники следует называть скорее невыпуклыми, чем вогнутыми, поскольку пересечение рёбер не образует новых вершин и все вершины находятся на окружности.
Выпуклые[править | править код]
Символ Шлефли {p} представляет правильный p-угольник.
| Название | Треугольник (2-симплекс) | Квадрат (2-ортоплекс) (2-куб) | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | |
|---|---|---|---|---|---|---|---|
| Шлефли | {3} | {4} | {5} | {6} | {7} | {8} | |
| Симметрия | D3, [3] | D4, [4] | D5, [5] | D6, [6] | D7, [7] | D8, [8] | |
| Коксетер | | |  |  |  |  | |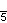
| Рисунок |  |  |  |  |  |  | |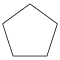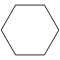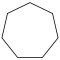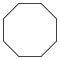
| Название | Девятиугольник | Десятиугольник | Одиннадцатиугольник | Двенадцатиугольник | Тринадцатиугольник | Четырнадцатиугольник | |
| Шлефли | {9} | {10} | {11} | {12} | {13} | {14} | |
| Симметрия | D9, [9] | D10, [10] | D11, [11] | D12, [12] | D13, [13] | D14, [14] | |
| Дынкин |  |  |  |  |  |  | |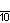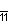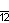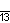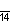
| Рисунок |  |  |  |  |  |  | |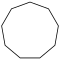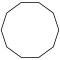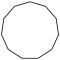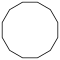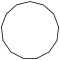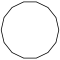
| Название | Пятнадцатиугольник | Шестнадцатиугольник | Семнадцатиугольник | Восемнадцатиугольник | Девятнадцатиугольник | Двадцатиугольник | …p-угольник |
| Шлефли | {15} | {16} | {17} | {18} | {19} | {20} | {p} |
| Симметрия | D15, [15] | D16, [16] | D17, [17] | D18, [18] | D19, [19] | D20, [20] | Dp, [p] |
| Дынкин |  |  |  |  |  |  | |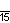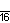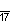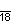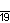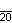
| Рисунок |  |  |  |  |  |  |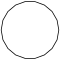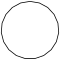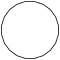
Сферические[править | править код]
Правильный двуугольник {2} можно считать вырожденным правильным многоугольником. Он может существовать как невырожденный в некоторых неевклидовых пространствах, таких как поверхность сферы или тора.
Звёзды[править | править код]
Существует бесконечно много правильных звёздчатых многогранников в двумерном пространстве (т.е. многоугольников), символы Шлефли которых являются рациональными числами {n/m}. Они называются звёздчатыми многоугольниками и имеют то же самое расположение вершин[en], что и у выпуклого многоугольника.
В общем случае для любого натурального числа n и для всех m, таких, что m < n/2 и m, n взаимно просты, существуют n-точечные правильные звёзды с символами Шлефли {n/m} (строго говоря, {n/m}={n/(n−m)}) .
Пространственные многоугольники[править | править код]
В 3-мерном пространстве правильный пространственный многоугольник [6] называется антипризматическим многоугольником и он имеет то же расположение вершин[en], что и у антипризмы, и его рёбра являются подмножеством рёбер антипризмы, соединяющие зигзагом вершины верхнего и нижнего многоугольников.
В 4-мерном пространстве правильный пространственный многоугольник может иметь вершины на торе Клиффорда и связан с вращением Клиффорда[en]. В отличие от антипризматичных пространственных многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.
Их можно видеть в многоугольниках Петри выпуклых правильных четырёхмерных многогранников[en], видимые как правильные плоские многоугольники периметров проекций Коксетера:
Трёхмерное пространство (многогранники)[править | править код]
В трёхмерном пространстве правильный многогранник с символом Шлефли {p,q} и диаграммой Коксетера 
имеет правильные грани вида {p} и правильную вершинную фигуру {q}.
Вершинная фигура (многогранника) является многоугольником, получаемым соединением вершин, отстоящих на одно ребро от заданной вершины. Для правильных трёхмерных многогранников, эта вершинная фигура является всегда правильным (и планарным) многоугольником.
Существование правильного многогранника {p,q} ограничено неравенством, относящимся к угловому дефекту вершинной фигуры:
- 1p+1q>12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}>{\frac {1}{2}}} : Многогранник (существует в евклидовом 3-мерном пространстве)
- 1p+1q=12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{2}}} : Евклидова плоская мозаика
- 1p+1q<12{\displaystyle {\frac {1}{p}}+{\frac {1}{q}}<{\frac {1}{2}}} : Замощение гиперболической плоскости
Перенумеровав перестановки, мы найдём 5 выпуклых форм, 4 звёздчатые формы и 3 плоских замощения, все с многоугольниками {p} и {q} из списка: {3}, {4}, {5}, {5/2} и {6}.
Вдобавок к мозаикам евклидова пространства существует бесконечное количество правильных гиперболических мозаик.
Выпуклые[править | править код]
Пять выпуклых правильных многогранников называются платоновыми телами. Вершинная фигура указана вместе с числом вершин. Все эти многогранники имеют эйлерову характеристику (χ) 2.